Tangente à une ellipse
2 participants
Page 1 sur 1
 Tangente à une ellipse
Tangente à une ellipse
Bonjour
Il y a déjà deux macros pour tracer la tangente à une courbe mais je propose d'avoir une troisième macro.
Dans la mesure où il y a une commande pour tracer un cercle ou une ellipse, on pourrait avoir une macro pour tracer la tangente à un cercle ou une conique déjà créé en un point donné par ces coordonnées cartésienne ou bien par un paramètre angulaire.
Il y a déjà deux macros pour tracer la tangente à une courbe mais je propose d'avoir une troisième macro.
Dans la mesure où il y a une commande pour tracer un cercle ou une ellipse, on pourrait avoir une macro pour tracer la tangente à un cercle ou une conique déjà créé en un point donné par ces coordonnées cartésienne ou bien par un paramètre angulaire.
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Bonjour Eric,
Le problème ici est qu'il faut se mettre d'accord sur la façon dont est défini le cercle ou l'ellipse. Par exemple on pourrait définir:
où on donne l'affixe du centre et l'affixe d'un point du cercle.
De même pour l'ellipse:
où on donne l'affixe du centre, un vecteur directeur du grand axe, le demi-grand axe, le demi-petit axe et un point de l'ellipse.
Le problème ici est qu'il faut se mettre d'accord sur la façon dont est défini le cercle ou l'ellipse. Par exemple on pourrait définir:
tangenteC( centre, point <,longueur> )
où on donne l'affixe du centre et l'affixe d'un point du cercle.
De même pour l'ellipse:
tangenteE( centre, direction grand axe, a, b, point <,longueur> )
où on donne l'affixe du centre, un vecteur directeur du grand axe, le demi-grand axe, le demi-petit axe et un point de l'ellipse.
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
En fait, il peut être plus pratique pour définir le point où on veut la tangente de donner sa position angulaire par rapport au grand axe pour l'ellipse (par rapport au rayon parallèle à l'horizontale pour le cercle ???).
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Pourquoi pas. On peut aussi pour allier les deux possiblités, mettre un système d'options:
point:=
angle:=
length:=
initialisées à Nil, et l'utlisateur donne soit le point soit l'angle (avec une priorité sur le point par exemple s'il donne les deux).
point:=
angle:=
length:=
initialisées à Nil, et l'utlisateur donne soit le point soit l'angle (avec une priorité sur le point par exemple s'il donne les deux).
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Il vaut peut être mieux donner la priorité à l'angle qui ne nécessite qu'un seul paramètre.
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Voilà une premièr proposition pour ces deux macros. J'ai mis un peu de temps car je veux que le tracé soit indépendant du changement de matrice et d'échelle. Par contre si le repère n'est pas orthonormé, il faut utiliser Rcercle et Rellipse pour avoir un cercle rond et la bonne ellipse.
Les deux macros:
a est le demi-grand axe (cm), b le demi-petit axe (cm), inclinaison est l'angle en degrés que fait le grand axe par rapport à l'horizontale.
Un exemple:
qui donne: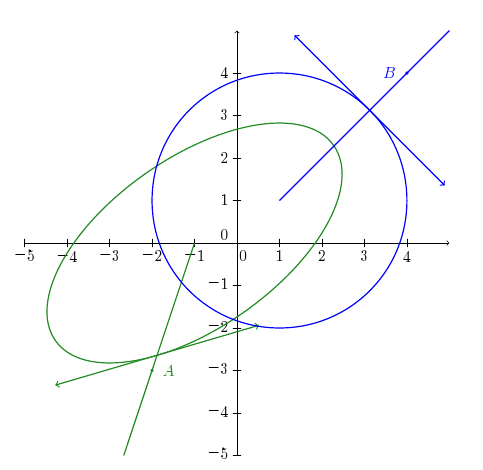
Comme on peut le voir, les points n'ont pas besoin d'être exactement sur le cercle ou l'ellipse.
Les deux macros:
tangenteC( centre, radius, [options]): tangente à un cercle
- Code:
{tangenteC( centre, radius, [options]): tangente à un cercle
options:
point:= affixe du point du cercle où on cherche la tangente (Nil par défaut)
angle:= angle en degrés que fait le point avec l'horizontale (Nil par défaut)
length:= longeur en cm (droite si length=Nil, c'est la valeur par défaut)
}
[$point:=Nil, $angle:=Nil, $length:=Nil, $radius:=%2, $centre:=%1,
SaveAttr(), $aux:=Eval(String(%3)),
if angle<>Nil then $A:=centre+ ScrCoordV(radius*exp(i*angle*deg))
else A:=centre+radius*(point-centre)/Abs(point-centre)
fi,
if length=Nil then Dperp([centre,A],A)
else
$u:=ScrCoordV(i*RealCoordV(A-centre)), u:=u/Abs(u),
Ligne([A-length/2*u, A+length/2*u],0)
fi,
RestoreAttr()
]
tangenteE( centre, a, b, inclinaison,[options]): tangente à une ellipse
a est le demi-grand axe (cm), b le demi-petit axe (cm), inclinaison est l'angle en degrés que fait le grand axe par rapport à l'horizontale.
- Code:
{tangenteE( centre, a, b, inclinaison,[options]): tangente à une ellipse
options:
point:= affixe du point de l'ellipse où on cherche la tangente (Nil par défaut)
angle:= angle en degrés que fait le point avec le grand axe (Nil par défaut)
length:= longeur en cm (droite si length=Nil, c'est la valeur par défaut)
}
[$point:=Nil, $angle:=Nil, $length:=Nil, $centre:=%1,
$inclinaison:=%4, $a:=%2, $b:=%3, $c:=sqrt(a^2-b^2),
SaveAttr(), $aux:=Eval(String(%5)),
if angle=Nil then point:=RealCoordV(point-centre)
else point:=exp(i*(angle+inclinaison)*deg)
fi,
SetMatrix([centre, 1/Xscale, i/Yscale]),
$dir:=exp(i*inclinaison*deg),
$M1:=matrix( affin(z, [0,dir],i*dir,a/b)),
$M2:=matrix( affin(z, [0,dir],i*dir,b/a)),
$u:=point/abs(point), $u':=mtransform(u,M1),
$A:=mtransform(a*u'/abs(u'), M2),
$F:=c*dir, $F':=-F,
$v:=(F'-A)/abs(F'-A)+(A-F)/abs(A-F), v:=v/abs(v),
if length=Nil then Droite(A,A+v)
else
Ligne([A-length/2*v, A+length/2*v],0)
fi,
RestoreAttr()
]
Un exemple:
- Code:
[
Arrows:=1, Width:=4, Axes(0,1+i), Arrows:=0,
Width:=8, Color:=forestgreen, Rellipse(-1,4,2,35),
A:=-2-3*i, LabelDot(A,"$A$","E",1), Ddroite(-1,A), Arrows:=2,
tangenteE(-1,4,2,35,[point:=A, length:=5]),
Arrows:=0, Color:=blue,
Rcercle(1+i,3), B:=4+4*i, LabelDot(B,"$B$","O",1), Ddroite(1+i,B), Arrows:=2,
tangenteC(1+i,3,[angle:=45, length:=5])
]
qui donne:

Comme on peut le voir, les points n'ont pas besoin d'être exactement sur le cercle ou l'ellipse.
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
J'ai commencé à expérimenter avec :
J'ai créé l'élément graphique
[
tangenteC(0,2,[point:=b,length:=3]),
tangenteC(0,2,[point:=c,length:=3]),
tangenteC(0,2,[point:=a,length:=3])
]
où
a=2*exp(i*2*pi/3)
b=1
c=2*exp(i*7*pi/5)
Comment puis-je maintenant tracer la perpendiculaire à la tangente en a passant par le milieux de [bc] ?
J'ai créé l'élément graphique
[
tangenteC(0,2,[point:=b,length:=3]),
tangenteC(0,2,[point:=c,length:=3]),
tangenteC(0,2,[point:=a,length:=3])
]
où
a=2*exp(i*2*pi/3)
b=1
c=2*exp(i*7*pi/5)
Comment puis-je maintenant tracer la perpendiculaire à la tangente en a passant par le milieux de [bc] ?
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Deux réponses possibles:
méthode bourrin: on extrait deux points de cette tangente et on trace la perpendiculaire passant par (b+c)/2
méthode géométrique: c'est la parallèle au rayon [0,a] passant par (b+c)/2
méthode bourrin: on extrait deux points de cette tangente et on trace la perpendiculaire passant par (b+c)/2
- Code:
Dperp( Get(tangenteC(0,2,[point:=a,length:=3]) ),(b+c)/2)
méthode géométrique: c'est la parallèle au rayon [0,a] passant par (b+c)/2
- Code:
Dparallel([0,a],(b+c)/2)
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Et hop, voila un théorème de Cantor illustré
On considère les tangentes au cercle circonscrit aux sommets du triangle. Les perpendiculaires à ces droites passant par les milieux des côtés opposés sont concourantes et elles se coupent au centre du cercle des neuf points.
Edit : remplacement du code pgf par le code TeXgraph.
- Code:
% TeXgraph version 1.94 beta-7.2
% Fenetre Xmin Xmax Ymin Ymax Xscale Yscale
100#-3#3#-3#3#1#1##
% Marges gauche droite haut bas cadre gestion_couleur comptgraph
101#0#0#0#0#0#1#4##
% Affectation des Variables theta et phi et type de perspective
18##[theta:=0.5236, phi:=1.0472,OriginalCoord(1),IdMatrix(),IdMatrix3D(),ModelView(ortho)]##
% Déclaration des Variables Globales
15#a#R*exp(i*2*pi/3)##
15#b#R##
15#c#R*exp(i*8*pi/7)##
15#R#2##
% Déclaration des Macros
16#tangenteC#{tangenteC( centre, radius, [options]): tangente à un cercle
options:
point:= affixe du point du cercle où on cherche la tangente (Nil par défaut)
angle:= angle en degrés que fait le point avec l'horizontale (Nil par défaut)
length:= longeur en cm (droite si length=Nil, c'est la valeur par défaut)
}
[$point:=Nil, $angle:=Nil, $length:=Nil, $radius:=%2, $centre:=%1,
SaveAttr(), $aux:=Eval(String(%3)),
if angle<>Nil then $A:=centre+ ScrCoordV(radius*exp(i*angle*deg))
else A:=centre+radius*(point-centre)/Abs(point-centre)
fi,
if length=Nil then Dperp([centre,A],A)
else
$u:=ScrCoordV(i*RealCoordV(A-centre)), u:=u/Abs(u),
Ligne([A-length/2*u, A+length/2*u],0)
fi,
RestoreAttr()
]##
% Déclaration des Eléments graphiques
% objet1 (Cercle)
7#objet1#[ 0,R ]##
% Laba (Utilisateur)
18##[tMin:=-5,tMax:=5]##
14#Laba#LabelDot(a,"$a$","N",1)#-1##
% Labb (Utilisateur)
14#Labb#LabelDot(b,"$b$","E",1)#-1##
% Labc (Utilisateur)
14#Labc#LabelDot(c,"$c$","SO",1)#-1##
% objet2 (Ligne Polyg.)
12#objet2#[ a,b,c ]#1#0##
% objet3 (Utilisateur)
14#objet3#[
tangenteC(0,R,[point:=b,length:=3]),
tangenteC(0,R,[point:=c,length:=3]),
tangenteC(0,R,[point:=a,length:=3]),
Dperp( Get(tangenteC(0,R,[point:=a,length:=3]) ),(b+c)/2),
Dperp( Get(tangenteC(0,R,[point:=b,length:=3]) ),(a+c)/2),
Dperp( Get(tangenteC(0,R,[point:=c,length:=3]) ),(a+b)/2),
]#-1##
On considère les tangentes au cercle circonscrit aux sommets du triangle. Les perpendiculaires à ces droites passant par les milieux des côtés opposés sont concourantes et elles se coupent au centre du cercle des neuf points.
Edit : remplacement du code pgf par le code TeXgraph.
Dernière édition par Eric Kouris le Ven 31 Oct - 1:30, édité 1 fois
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
C'est joli ça! Tu n'arrêtes donc jamais?
Au fait tu as vu le dernier post sur le réarrangement? Avec une vraie définition de matheux c'est nettement mieux non?
Au fait tu as vu le dernier post sur le réarrangement? Avec une vraie définition de matheux c'est nettement mieux non?
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
P.Fradin a écrit:C'est joli ça! Tu n'arrêtes donc jamais?
J'ai une idée de projet sur de la géométrie, pour l'instant je profite que j'ai du temps pour voir si c'est faisable dans un temps raisonnable.
Au fait tu as vu le dernier post sur le réarrangement? Avec une vraie définition de matheux c'est nettement mieux non?
J'ai vu, il faut que je remplace l'ancien code par le nouveau dans le fichier (j'avais modifié la fonction initiale).
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Et une généralisation du théorème précédent
ici avec un quadrilatère mais on peut le faire avec un polygone à n côtés (on perd le cercle des neuf points dans la généralisation).
- Code:
% TeXgraph version 1.94 beta-7.2
% Fenetre Xmin Xmax Ymin Ymax Xscale Yscale
100#-3#3#-3#3#1#1##
% Marges gauche droite haut bas cadre gestion_couleur comptgraph
101#0#0#0#0#0#1#4##
% Affectation des Variables theta et phi et type de perspective
18##[theta:=0.5236, phi:=1.0472,OriginalCoord(1),IdMatrix(),IdMatrix3D(),ModelView(ortho)]##
% Déclaration des Variables Globales
15#a#R*exp(i*2*pi/3)##
15#b#R##
15#c#R*exp(i*11*pi/7)##
15#R#2##
15#d#R*exp(i*8*pi/7)##
% Déclaration des Macros
16#tangenteC#{tangenteC( centre, radius, [options]): tangente à un cercle
options:
point:= affixe du point du cercle où on cherche la tangente (Nil par défaut)
angle:= angle en degrés que fait le point avec l'horizontale (Nil par défaut)
length:= longeur en cm (droite si length=Nil, c'est la valeur par défaut)
}
[$point:=Nil, $angle:=Nil, $length:=Nil, $radius:=%2, $centre:=%1,
SaveAttr(), $aux:=Eval(String(%3)),
if angle<>Nil then $A:=centre+ ScrCoordV(radius*exp(i*angle*deg))
else A:=centre+radius*(point-centre)/Abs(point-centre)
fi,
if length=Nil then Dperp([centre,A],A)
else
$u:=ScrCoordV(i*RealCoordV(A-centre)), u:=u/Abs(u),
Ligne([A-length/2*u, A+length/2*u],0)
fi,
RestoreAttr()
]##
% Déclaration des Eléments graphiques
% objet1 (Cercle)
7#objet1#[ 0,R ]##
% Laba (Utilisateur)
18##[tMin:=-5,tMax:=5]##
14#Laba#LabelDot(a,"$a$","N",1)#-1##
% Labb (Utilisateur)
14#Labb#LabelDot(b,"$b$","E",1)#-1##
% Labc (Utilisateur)
14#Labc#LabelDot(c,"$c$","SO",1)#-1##
% objet2 (Ligne Polyg.)
12#objet2#[ a,b,c,d ]#1#0##
% objet3 (Utilisateur)
14#objet3#[
tangenteC(0,R,[point:=b,length:=3]),
tangenteC(0,R,[point:=c,length:=3]),
tangenteC(0,R,[point:=a,length:=3]),
tangenteC(0,R,[point:=d,length:=3]),
Dperp( Get(tangenteC(0,R,[point:=a,length:=3]) ),(b+c+d)/3),
Dperp( Get(tangenteC(0,R,[point:=b,length:=3]) ),(a+c+d)/3),
Dperp( Get(tangenteC(0,R,[point:=c,length:=3]) ),(a+b+d)/3),
Dperp( Get(tangenteC(0,R,[point:=d,length:=3]) ),(a+b+c)/3),
]#-1##
% Labd (Utilisateur)
18##[tMin:=-3,tMax:=3]##
14#Labd#LabelDot(d,"$d$","S",1)#-1##
ici avec un quadrilatère mais on peut le faire avec un polygone à n côtés (on perd le cercle des neuf points dans la généralisation).
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Juste une question:
pourquoi pour tracer la perpendiculaire à une tangente tu prends la méthode graphique que j'ai qualifiée de "bourrine" et pas la méthode géométrique?
pourquoi pour tracer la perpendiculaire à une tangente tu prends la méthode graphique que j'ai qualifiée de "bourrine" et pas la méthode géométrique?
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Finalement je suis revenu en arrière, je propose ici une version des deux macros sensible aux changements de matrice et d'échelle, ce qui permet de zoomer avec la souris (ou les boutons de zoom + et -). Bien sûr, si le repère n'est pas orthonormé, les cercles ne sont plus ronds et les ellipses changent de forme, mais cela reste de toute façon des ellipses et comme les applications affines conservent les tangentes, la figure reste correcte.
PS: cela m'a permis de déceler une coquille dans la macro ellipse, mais qui n'a d'incidence que lorsque le repère n'est pas orthonormé. Cela sera rectifié dans la prochaine version.
- Code:
{tangenteC( centre, radius, [options]): tangente à un cercle
options:
point:= affixe du point du cercle où on cherche la tangente (Nil par défaut)
angle:= angle en degrés que fait le point avec l'horizontale (Nil par défaut)
length:= longeur en cm (droite si length=Nil, c'est la valeur par défaut)
}
[$point:=Nil, $angle:=Nil, $length:=Nil, $radius:=%2, $centre:=%1,
SaveAttr(), $aux:=Eval(String(%3)),
if angle<>Nil then $A:=centre+ radius*exp(i*angle*deg)
else A:=centre+radius*(point-centre)/abs(point-centre)
fi,
if length=Nil then Dperp([centre,A],A)
else
$u:=i*(A-centre), u:=u/abs(u),
Ligne([A-length/2*u, A+length/2*u],0)
fi,
RestoreAttr()
]
- Code:
{tangenteE( centre, a, b, inclinaison,[options]): tangente à une ellipse
options:
point:= affixe du point de l'ellipse où on cherche la tangente (Nil par défaut)
angle:= angle en degrés que fait le point avec le grand axe (Nil par défaut)
length:= longeur en cm (droite si length=Nil, c'est la valeur par défaut)
}
[$point:=Nil, $angle:=Nil, $length:=Nil, $centre:=%1,
$inclinaison:=%4, $a:=%2, $b:=%3, $c:=sqrt(a^2-b^2),
SaveAttr(), $aux:=Eval(String(%5)),
if angle=Nil then point:=point-centre
else point:=exp(i*(angle+inclinaison)*deg)
fi,
ComposeMatrix([centre, 1, i]),
$dir:=exp(i*inclinaison*deg),
$M1:=matrix( matrix(affin(z, [0, dir],i*dir,a/b))),
$M2:=matrix( matrix( affin(z, [0, dir],i*dir,b/a))),
$u:=mtransform(point,M1),
$A:=mtransform(a*u/abs(u), M2),
$F:=c*dir, $F':=-F,
$v:=(F'-A)/abs(F'-A)+(A-F)/abs(A-F), v:=v/abs(v),
if length=Nil then Droite(A,A+v)
else
Ligne([A-length/2*v, A+length/2*v],0)
fi,
RestoreAttr()
]
PS: cela m'a permis de déceler une coquille dans la macro ellipse, mais qui n'a d'incidence que lorsque le repère n'est pas orthonormé. Cela sera rectifié dans la prochaine version.
 Re: Tangente à une ellipse
Re: Tangente à une ellipse
Je précise au passage que le théorème précédent est dû à Moritz Benedikt Cantor (1829-1920) et non pas à Georg Cantor (1845-1918).
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum|
|
|
